(Apologies for the rather incoherent nature of this post — I’m trying, as an experiment to push myself to post more, to “write more quickly”, so a lot of things here are not explained in a way that makes sense and some of it is even nonsensical: forget “polishing” for precision or clarity; I haven’t even written it down reasonably the first time. But whatever…)
Since last week I’ve been attending a weekly “meetup” (book club / study group) for studying TAOCP (The Art of Computer Programming by Donald Knuth). Today, we were reading about Huffman trees, and Arthur O’Dwyer (through whose blog I learned of this meetup, just before last week’s meeting) brought up an interesting question.
Suppose you take a set of several items, and play “Twenty Questions” on it with your friend. That is, at each step you pick a subset of these items and ask your friend whether or not her chosen item is in that set. (Equivalently: at each step you partition the set of items into two sets, and ask which of the two sets the item lies in.) Suppose you also know the probabilities with which the items will be picked. (This is different from the usual setting, which is adversarial.) Then what should your (deterministic) algorithm (decision tree) be: which question should you ask first, and then (depending on the answer) which question do you ask next, and so on?
Now, Huffman’s algorithm is precisely the provably optimal solution to this problem: it gives a tree that has minimum expected number of questions.
If we didn’t have Huffman coding on our mind, we might think of something like this:
-
Partition the set of items into two sets, such that the total probability of each set (sum of the probabilities of the individual items in the set) is as close as possible to the other. (This is already a hard problem computationally: it’s the number-partitioning problem, a special case of the subset-sum problem which is a special case of the knapsack problem. For a popular exposition, see the nice article “The Easiest Hard Problem” by Brian Hayes.)
-
Depending on the answer (which of the two sets the item lies in), repeat.
So the question he raised is:
-
Is this method equivalent to Huffman’s, i.e. does it always give the same/equivalent tree? (Turns out no; we looked at an example where the tree would be different, but in that case it turned out that the tree still has the same total weighted path length.)
-
Ok, maybe the tree would be different, but does this method always give an optimal solution as well?
I “started” to try to come up with examples on my own, but in the meantime (alas, problem-solving skills atrophy in the presence of an internet connection: see also this and this that I encountered recently) I looked up the Wikipedia article, which in the second paragraph of the “History” section points out:
In doing so, Huffman outdid Fano, who had worked with information theory inventor Claude Shannon to develop a similar code. Building the tree from the bottom up guaranteed optimality, unlike the top-down approach of Shannon–Fano coding.
Aha. Following the link to “Shannon–Fano coding” reveals something that seems exactly like our question:
Fano’s method divides the source symbols into two sets (“0” and “1”) with probabilities as close to 1/2 as possible. Then those sets are themselves divided in two, and so on, until each set contains only one symbol. The codeword for that symbol is the string of “0"s and “1"s that records which half of the divides it fell on. This method was proposed in a later technical report by Fano (1949).
But reading further down, it appears that this method does not consider all possible ways of partitioning (which would be computationally intractable for large n) but instead just splits the sorted list at a point where the two sublists have closest probability to each other.
Nevertheless, I took their example and tweaked it slightly to remove duplicates, and it turns out to be a counterexample (thus answering our question in the negative):
Consider {5, 6, 7, 8, 14}.
They add up to 40, and can be divided into two sets of exactly 20: {5, 7, 8} and {6, 14}. The former can be divided into {8} and {5, 7}. This gives the tree:
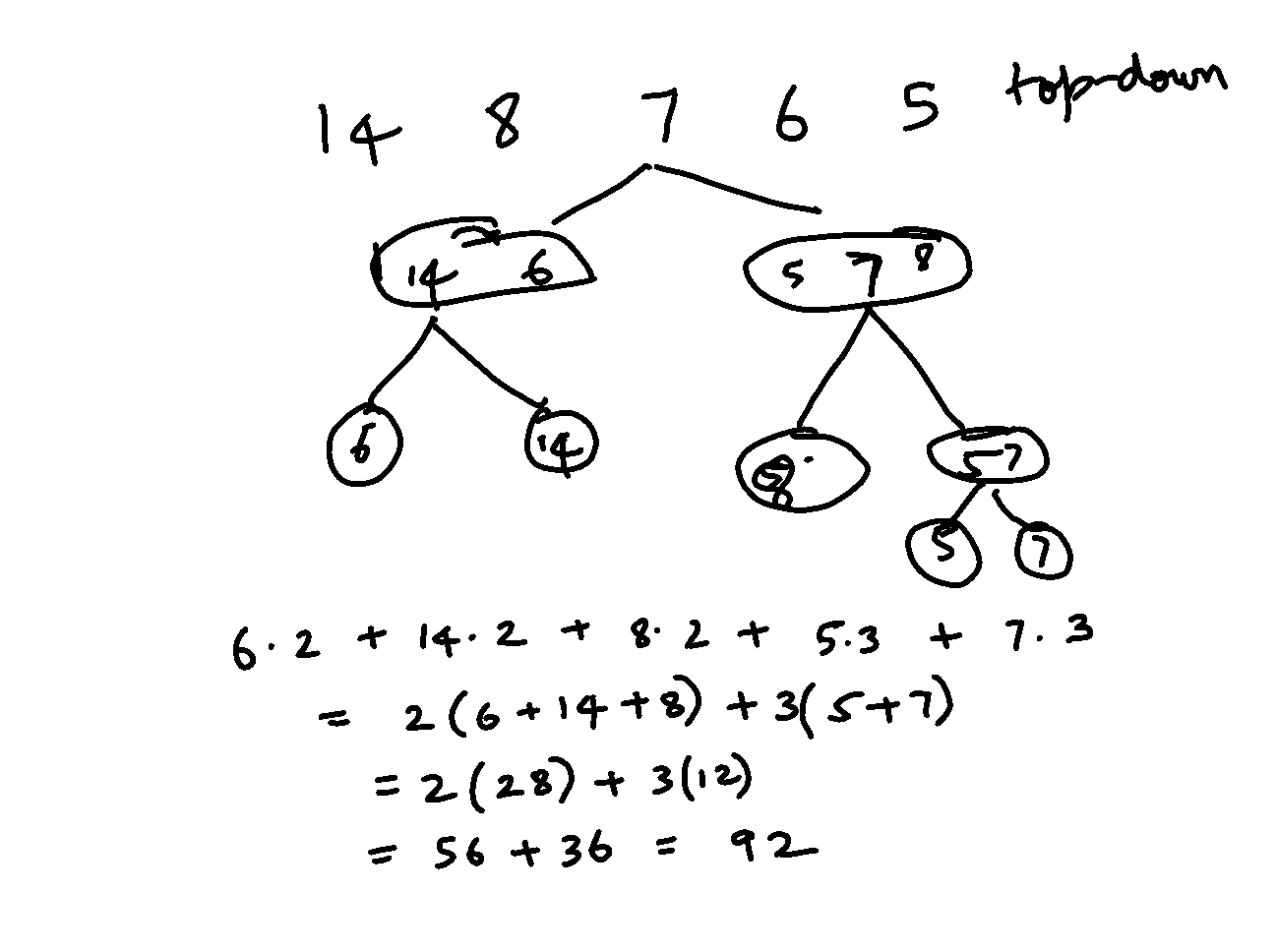
but Huffman would give the tree:
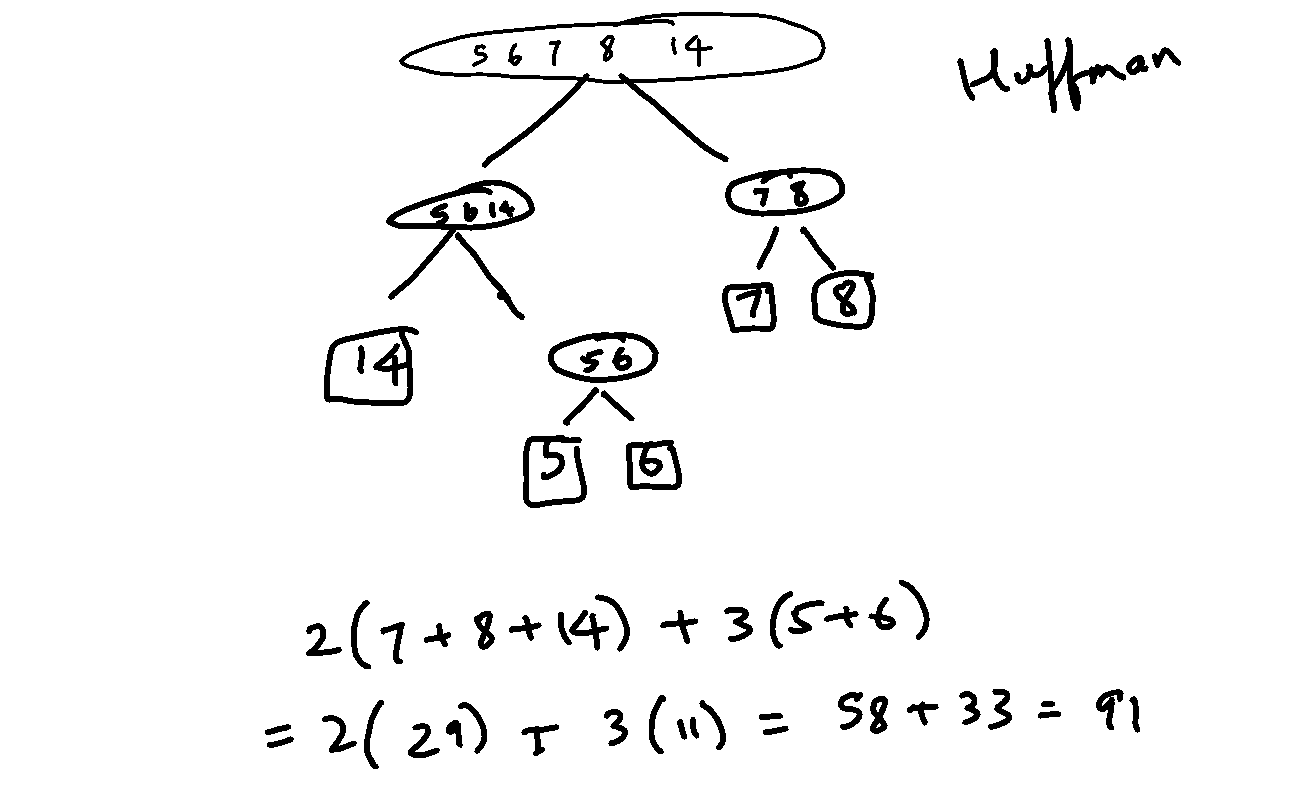
Actually, if you don’t mind the duplicates (why should you? Also note they are just probabilities…), even the example in the Wikipedia article works: consider {5, 6, 6, 7, 15}
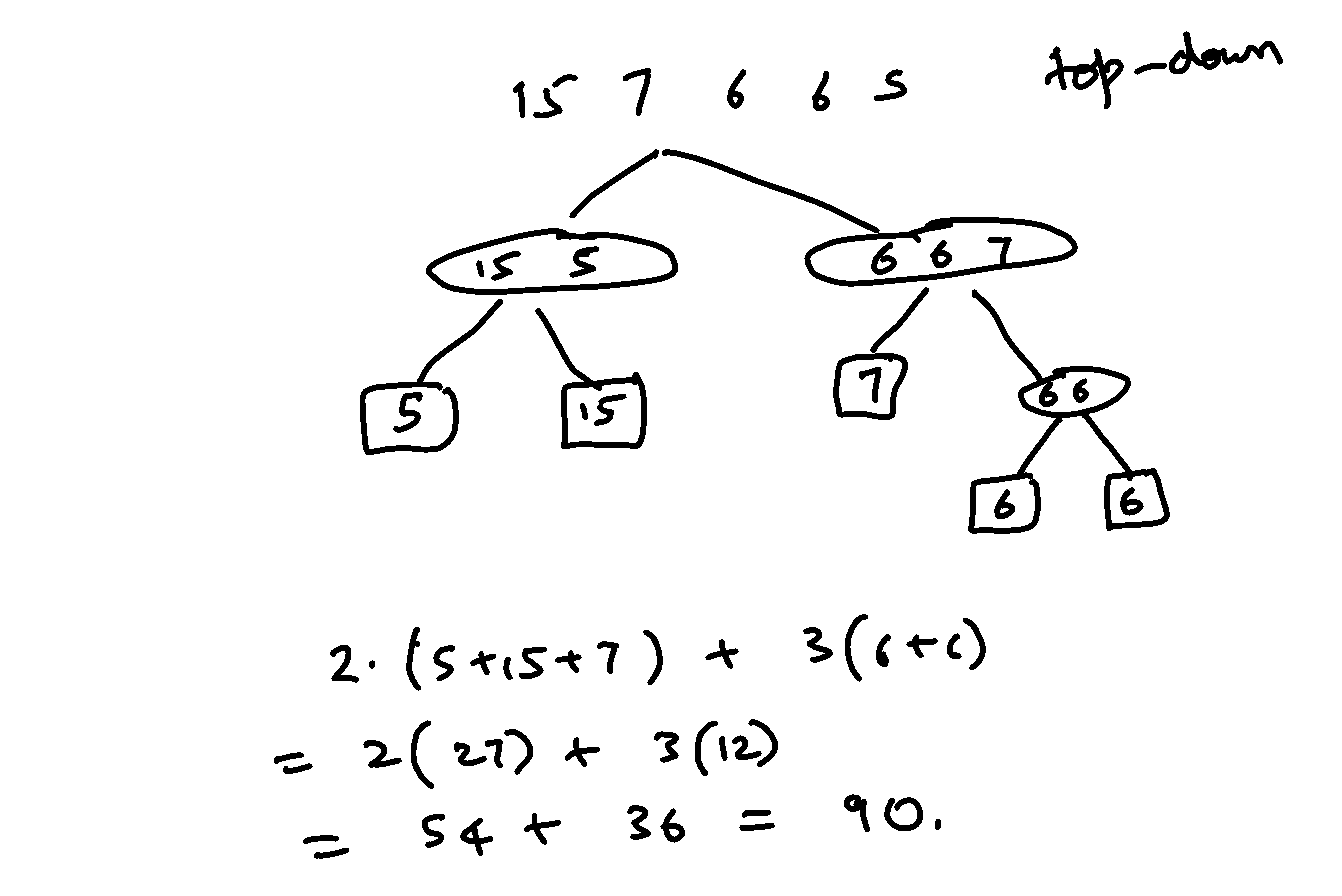
versus Huffman’s:
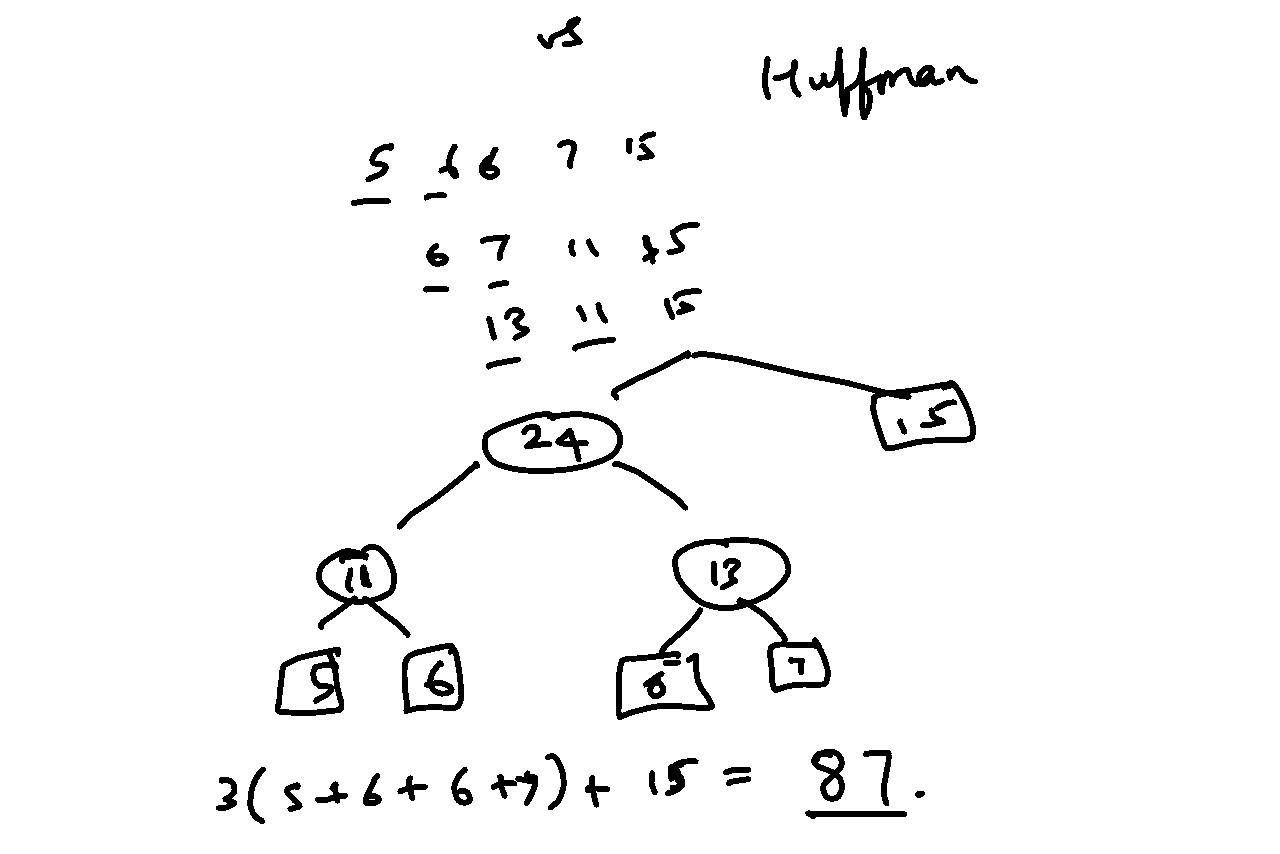
PS: While looking into this I came across an online subset-sum solver (GitHub). It seems to be more or less doing the brute-force thing (so much for the claim of “fastest”), but it’s useful to have such tools for specific problems available online via a web interface.