Certifying that M_127 is prime

Let $M_p=2^p-1$, so that:

$$\begin{array}{rl}{M}_2& =2^2-1=4-1=3\\ M_3& =2^3-1=8-1=7\\ M_7& =2^7-1=128-1=127\\ M_{127}& =2^{127}-1\end{array}$$

Is $M_{127}$ prime? This is a large number with 39 digits, specifically it is 170141183460469231731687303715884105727.

We can just look up what is known: the Wikipedia article on Mersenne prime links to OEIS A000043, “primes p such that 2^p - 1 is prime”, a list which contains $127$. In fact, the “List of Known Mersenne Prime Numbers” on mersenne.org says that $M{}_1{}_2{}_7$ was declared prime by Édouard Lucas a long time ago, in January 1876. The page does not mention it, but he came to this conclusion after hundreds of hours spent doing binary arithmetic by placing pawns on a very large chessboard (of size $127\times 127$); there’s a demonstration of his “game” in these slides, and a fuller account in Factoring Integers Before Computers (1994) by H. C. Williams and J. O. Shallit, in Mathematics of Computation, 1943–1993: A Half-century of Computational Mathematics (which is Proceedings of Symposia in Applied Math., Vol 48, ed. Walter Gautschi, publ. AMS). (Williams also has a book/monograph about Lucas that goes into some detail.)

So yes, $2^{127}-1$ is prime. Even Wolfram Alpha knows this:

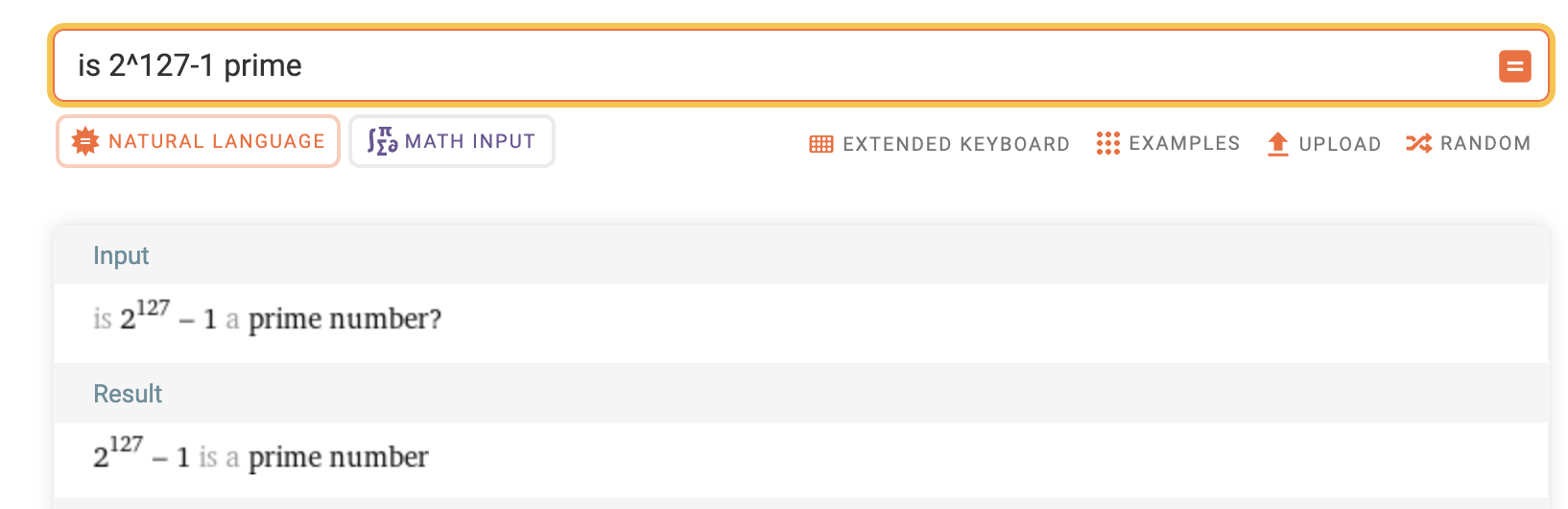
But if someone doesn’t want to rely on published knowledge or a computer algebra system like Wolfram Alpha, could we convince them that $M_{127}$ is prime? More generally, is there a short certificate that a number is prime?

Think about that for a moment: if you want to convince someone that a number is not prime, all you have to do is give them a nontrivial factor. But how can you give a certificate that a number is not prime?

(In the days before the AKS primality test aka $\mathsf{PRIMES}\in \text{P}$, in the terminology of computational complexity theory, we’d say this as: it is easy to see that $\mathsf{PRIMES}\in \text{co-NP}$. But does $\mathsf{PRIMES}\in \text{NP}$ as well?)

In 1975, Vaughan Pratt (the same Pratt in “Knuth–Morris–Pratt” and “Pratt parser”) found a way, which relies on the Lucas primality test:

Lucas' theorem: Suppose we have an integer $a$ such that:

• $a^{n-1}\equiv 1(\mathrm{mod}n)$, and
• $a^{(n-1)/q}\not\equiv 1(\mathrm{mod}n)$ for every prime factor $q$ of $n-1$

Then $n$ is prime.

(Such an $a$ is called a witness.)

We assume that the person we’re trying to convince understands the theorem above, and is good at computation and/or can use computers/calculators for simple straightforward calculations (like multiplication, exponentiation, and modular arithmetic), but does not trust complicated algorithms implemented inside computer algebra systems that would take a long time to read and verify.

So first we get the factorization of $n-1$ from wherever, and verify that: $$M_{127}-1=2\times 3^3\times 7^2\times 19\times 43\times 73\times 127\times 337\times 5419\times 92737\times 649657\times 77158673929$$

import math
s = [2, 3, 3, 3, 7, 7, 19, 43, 73, 127, 337, 5419, 92737, 649657, 77158673929]
l1 = math.prod(s)
l2 = 2**127 - 2
print(l1)
print(l2)
print(l1 == l2)

Then, to prove that $M_{127}$ is prime, we have to find such an $a$ (a witness).

Let’s try to find one, with brute force. Here, $n=M_{127}$.

import math
n = 2**127 - 1
s = [2, 3, 3, 3, 7, 7, 19, 43, 73, 127, 337, 5419, 92737, 649657, 77158673929]
assert math.prod(s) == n - 1
witness = None
for a in range(1, n):
  if (pow(a, n - 1, mod=n) == 1 and
    all(pow(a, (n - 1)//q, mod=n) != 1 for q in s)):
    witness = a
    break
print(witness)

This prints $43$.

This is a certificate to convince our sceptical friend: all we need to give them is the above list of prime factors of $n-1$ and the witness $a=43$, and they can verify that indeed it is true that $a^{n-1}\equiv 1(\mathrm{mod}n)$, but $a^{(n-1)/q}\not\equiv 1(\mathrm{mod}n)$ for any $q$ in the list, and therefore by the theorem of Lucas, $n$ is prime.

But wait, says our friend: how do I know that you aren’t trying to trick me by giving some large composite numbers in the list of “prime” factors: how do I know that (say) 77158673929 is actually prime?

The answer is that we can certify it (recursively) in the same way!

This is the idea behind Pratt’s primality certificate. For this example, let’s find a complete certificate. For the purposes of this blog post, we’ll not bother with a factoring algorithm here, and hard-code every factorization we’ll need, obtained from elsewhere (it does not matter, as everything will be verified by our friend):

import math

def witness(n, factors):
  for a in range(1, n):
    if (pow(a, n - 1, mod=n) == 1 and
      all(pow(a, (n - 1)//q, mod=n) != 1 for q in factors)):
      return a

def certificate(n):
  factors = known_factors[n-1]
  assert math.prod(factors) == n - 1
  a = witness(n, factors)
  if not a: return None
  certificates = [certificate(q) for q in factors]
  return {'p': n, 'witness': a, 'primes': certificates}

known_factors = {
  1: [],
  2: [2],
  4: [2, 2],
  6: [2, 3],
  10: [2, 5],
  18: [2, 3, 3],
  22: [2, 11],
  42: [2, 3, 7],
  72: [2, 2, 2, 3, 3],
  126: [2, 3, 3, 7],
  336: [2, 2, 2, 2, 3, 7],
  1288: [2, 2, 2, 7, 23],
  5418: [2, 3, 3, 7, 43],
  92736: [2, 2, 2, 2, 2, 2, 3, 3, 7, 23],
  174762: [2, 3, 3, 7, 19, 73],
  649656: [2, 2, 2, 3, 3, 7, 1289],
  699052: [2, 2, 174763],
  77158673928: [2, 2, 2, 3, 3, 3, 7, 73, 699053],
  170141183460469231731687303715884105726: [2, 3, 3, 3, 7, 7, 19, 43, 73, 127, 337, 5419, 92737, 649657, 77158673929],
}

n = 2**127 - 1
printed = set()
def cprint(cert, indent):
  p = cert['p']
  print(indent, p)
  if p in printed or p < 1000: return
  printed.add(p)
  print(indent, '-> Witness', cert['witness'], 'with primes:')
  for qc in cert['primes']:
    cprint(qc, indent + '        ')
cprint(certificate(n), '')

The (large) output of the program above amounts to a verifiable certificate that $M_{127}$ is prime — to keep the output small, the program above leaves out certificates for primes less than 1000:

 170141183460469231731687303715884105727
 -> Witness 43 with primes:
         2
         3
         3
         3
         7
         7
         19
         43
         73
         127
         337
         5419
         -> Witness 3 with primes:
                 2
                 3
                 3
                 7
                 43
         92737
         -> Witness 5 with primes:
                 2
                 2
                 2
                 2
                 2
                 2
                 3
                 3
                 7
                 23
         649657
         -> Witness 5 with primes:
                 2
                 2
                 2
                 3
                 3
                 7
                 1289
                 -> Witness 6 with primes:
                         2
                         2
                         2
                         7
                         23
         77158673929
         -> Witness 11 with primes:
                 2
                 2
                 2
                 3
                 3
                 3
                 7
                 73
                 699053
                 -> Witness 2 with primes:
                         2
                         2
                         174763
                         -> Witness 17 with primes:
                                 2
                                 3
                                 3
                                 7
                                 19
                                 73

In the output above, our friend can verify that any particular number $p$ (like, say $77158673929$) is prime, by verifying that the primes listed under it do indeed multipy to $p-1$ (check: $2^3\times 3^3\times 7\times 73\times 699053=77158673928$), and that for the given witness $a$ the properties hold (check: ${11}^{77158673928}\equiv 1(\mathrm{mod}77158673929)$, and ${11}^{77158673928/73}\not\equiv 1(\mathrm{mod}77158673929)$ etc).

Further work: turn this into an interactive webpage, where clicking on any prime will show a certificate of primality for it.